Abstract

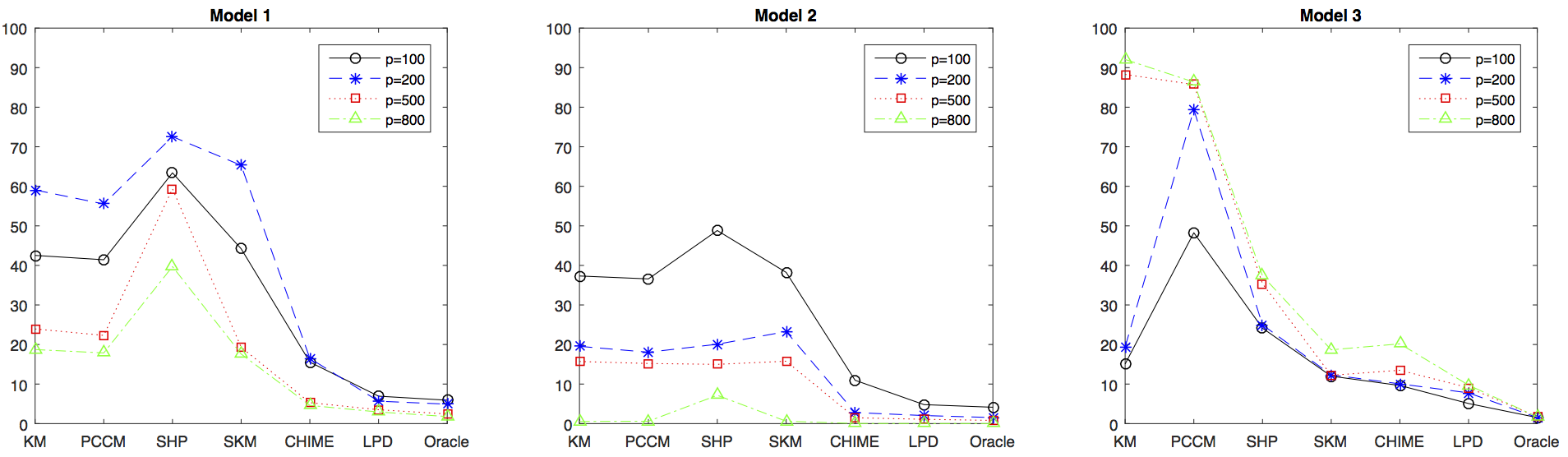
Unsupervised learning is an important problem in statistics and machine learning with a wide range of applications. In this paper, we study clustering of high-dimensional Gaussian mixtures and propose a procedure, called CHIME, that is based on the EM algorithm and a direct estimation method for the sparse discriminant vector. Both theoretical and numerical properties of CHIME are investigated. We establish the optimal rate of convergence for the excess mis-clustering error and show that CHIME is minimax rate optimal. In addition, the optimality of the proposed estimator of the discriminant vector is also established. Simulation studies show that CHIME outperforms the existing methods under a variety of settings. The proposed CHIME procedure is also illustrated in an analysis of a glioblastoma gene expression data set and shown to have superior performance.

Clustering of Gaussian mixtures in the conventional low-dimensional setting is also considered. The technical tools developed for the high-dimensional setting are used to establish the optimality of the clustering procedure that is based on the classical EM algorithm.

Keywords Clustering, Gaussian mixtures, linear discriminant analysis, mis-clustering error, optimality.